11428. Tree diameter

A tree consisting of n vertices is given.

The diameter of a tree is the maximum distance between two vertices. Find the diameter of the given tree.

Input. The first line contains an integer n (1 ≤ n ≤ 2 * 10⁵) – the number of vertices in the tree. The vertices are numbered from 1 to n.

Each of the following n – 1 lines describes an edge and contains two integers a and b (1 ≤ a, b ≤ n), indicating that there is an edge between vertices a and b.

Output. Print one integer – the diameter of the tree.

Sample input	Sample output
5 1 2 1 3 3 4 3 5	3

SOLUTION

graphs – depth first search

Algorithm analysis

Perform a depth-first search starting from any vertex, for example, from vertex 1. Find the vertex farthest from 1 and denote it as vertex a. Then, start a depth-first search from vertex a to find the vertex that is farthest from a, which we’ll denote as vertex b. The distance between vertices a and b will then be the maximum possible and equal to the diameter of the tree.

Example

Consider the tree from the example.

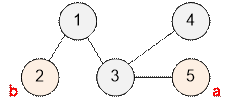
The diameter of the tree is 3. The maximum distance is achieved, for example, between vertices 2 and 5.

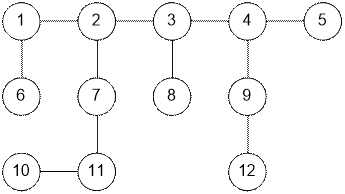
Exercise

Find the diameter of the tree.

Algorithm implementation

Store the input tree in the adjacency list g. Store the shortest distances from the source to each vertex in the array dist.

vector<vector<int>> g;

vector<int> dist;

The dfs function performs a depth-first search from vertex v. The shortest distance from the source to vertex v is d. The parent of vertex v in the depth-first search is p.

void dfs(int v, int d, int p = -1)

{

Store the shortest distance from the source to vertex v in dist[v].

dist[v] = d;

Iterate over all edges (v, to). For each son to of vertex v (where to is not a parent of v) initiate a depth-first search. The distance from the source to vertex to will be d + 1.

for (int to : g[v])

if (to != p) dfs(to, d + 1, v);

}

The main part of the program. Read the input data.

scanf("%d", &n);

g.resize(n + 1);

dist.resize(n + 1);

Construct an undirected tree.

for (i = 1; i < n; i++)

{

scanf("%d %d", &u, &v);

g[u].push_back(v);

g[v].push_back(u);

}

Find the shortest distances from vertex 1 to all other vertices. The vertex farthest from it is a.

dfs(1, 0, -1);

a = max_element(dist.begin(), dist.begin() + n + 1) –

dist.begin();

Find the shortest distances from vertex b to all other vertices. The vertex farthest from it is b.

dfs(a, 0, -1);

b = max_element(dist.begin(), dist.begin() + n + 1) –

dist.begin();

Print the diameter of the tree – the shortest distance from a to b.

printf("%d\n", dist[b]);